• View
• Edit
• History
• Print

RadiusRechner

nach einer Idee in GARTENBAHNEN von K Rabensdorf (1/98), H-J Kabbe (1/99) und R Erteld (2/04)
siehe auch GARTENBAHNEN 1/00: M & S BAUM: Pythagoras statt Vogel, die Seitenverschiebung von Achsen in einem Starrrahmen

Für Gartenbahner ein total unerlässlicher Rechner: Wenn Sie nur drei Meter gebogenes Gleis haben - wie gross ist dann der Radius? Oder etwas theoretischer gesagt: Im Gelände ist es nicht so einfach, den Mittelpunkt eines Kreises zu finden, wenn man nur einen kleinen Teil des Bogens kennt. Dieser Rechner schliesst von der Höhe des Bogens auf den Radius, beziehungsweise umgekehrt, vom Radius auf die Höhe des Bogens.

Hier kommen Sie direkt zu den beiden Rechnern:

1. Sie kennen den Radius - wie gross ist die Höhe des Bogens? [H-[Hilfe/X.Radius2|--> Radius nach Bogenhöhe-Rechner]]
2. Sie kennen die Höhe des Bogens - wie gross ist der Radius? --> Bogenhöhe nach Radius-Rechner

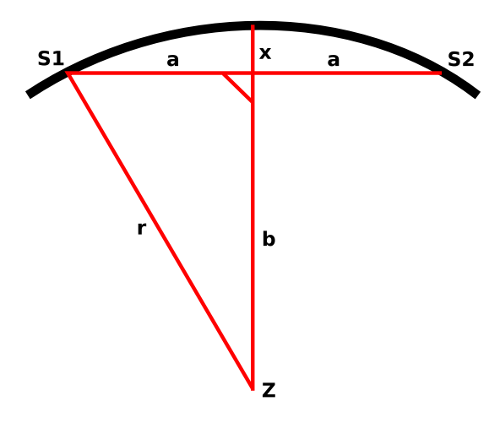die Theorie

Die Sache ist mit etwas Algebra zu lösen. Die Rechnerei nehmen Ihnen dann meine beiden Rechner ab, denn mit dem Taschenrechner ist das ziemlich umständlich.

Im nebenstehenden Bild gehört der schwarze Kreisbogen zu einem Kreis, von dem wir weder Mittelpunkt noch Radius kennen. Über der Sehne S1-S2 spannt sich der Bogen mit der Sehenenlänge 2a und der Bogenhöhe x. Zum virtuellen Mittelpunkt hin entsteht ein rechtwinkliges Dreieck bestehend aus dem Radius r, der halben Sehne a und der Geraden b. Darin gilt:

    r² = a²+b²      und      r = x+b
 also
    r² = a²+b² = (b+x)² = b²+2bx+x²

 Fall 1: Auflösung nach der Bogenhöhe:
    b² = r²-a²
    x = r-√(r²-a²)

 Fall 2: Auflösung nach dem Radius:
    a²+b² = b²+2bx+x²  -->  a² = 2bx+x²
    a²/x = 2b+x  -->  a²/x -x = 2b  -->  (a²/x-x)/2 = b
    r = b+x = ((a²/x -x)/2) +x

Ich hoffe, dass alles richtig ist...

die Funktion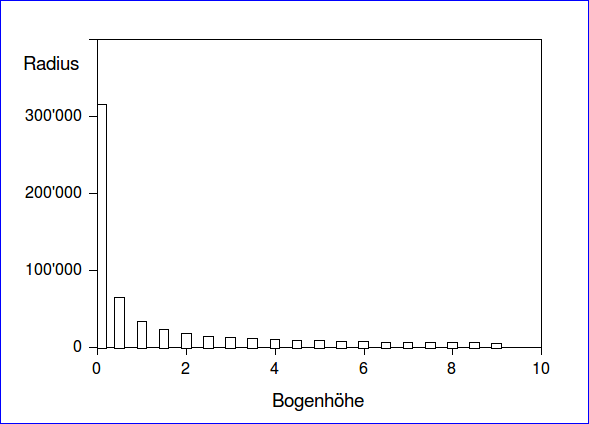

Die Funktion ist quadratisch, wenn die Bogenhöhe gegen Null strebt, geht der Radius gegen unendlich. Was unmittelbar einleuchtet: Eine Kurve mit dem Radius unendlich ist eben eine Gerade. Für eine Sehnenlänge von 500mm sieht das so aus (Masse in mm) und die Grafik veranschaulicht die Sache:

 Bogenhöhe   Radius
 ------------------------------------------------------------------
     0.1    312'500
     0.5     62'500
     1.0     31'250      im Bereich der grossen Radien entspricht
     1.5     20'834      1mm Bogenhöhen-Differenz etwa 15m Radius-
     2.0     15'626      unterschied
     2.5     12'501
     3.0     10'418
     4.0      7'815
     4.5      6'947
     5.0      6'253
     5.5      5'685
     6.0      5'211
     6.5      4'840
     7.0      4'468      im Bereich der kleinen Radien entspricht
     7.5      4'190      1mm Bpgenhöhen-Differenz etwa 1.5m 
     8.0      3'910      Radiusunterschied
 ------------------------------------------------------------------

das Messgerät

Wenn Sie versuchen, die Bogenhöhe zu messen, stossen Sie vor allem bei grossen Radien auf Schwierigkeiten. Eine Messlatte von 50 oder 100cm Länge ergibt Bogenhöhen von einigen Millimetern, die kaum genau zu messen sind. Ich habe mir darum ein Messgerät gebaut, das die Bogenhöhe recht genau erfasst und auf einer Skala anzeigt.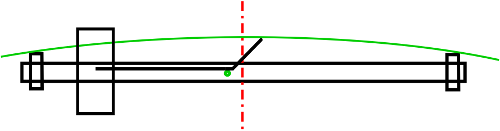

Der Stab ist ein Aluminium-Vierkantrohr 11x11x1.5 in das an beiden Enden starke Magnete eingeklebt sind. Der Zeiger ist etwa 130...140° gekröpft, er wird durch eine Feder im Zustand 'maximale Bogenhöhe' gehalten. Die Kröpfung linearisiert die Anzeige auf der Skala, sie wird beinahe linear. Dies geht allerdings auf Kosten der Genauigkeit: Die Messung erfolgt nicht genau in der Mitte zwischen den beiden Magneten.

Die Eichung nehmen Sie so vor:

• legen Sie das Gerät an ein gerades Eisenprofil und verstärken Sie den Halt durch zwei Gummibänder. Der Zeiger sollte jetzt oben auf der Skala stehen, biegen Sie ihn zurecht, wenn das nicht so ist; bezeichnen Sie diesen Punkt, es ist die Bogenhöhe Null entsprechend dem Radius unendlich
• jetzt unterlegen Sie beim einen Magneten einen Spiralbohrer von 1mm Durchmesser und erzeugen damit eine Bogenhöhe von der Hälfte des Bohrer-Durchmessers, also 0.5mm; dieser Punkt wird wieder auf der Skala bezeichnet
• fahren Sie weiter bis 16 oder 18mm Bohrerdicke, also 8...9mm Bogenhöhe, was Radien um 4m entspricht
• zeichnen Sie von Hand oder mit einem Zeichenprogramm eine hübsche Skala - fertig!

Klar, das ist die Eichung nach Art des armen Mannes und Alternativen gibt es sicher mehrere. Zum Beispiel mit einer Schiebelehre oder einem Mikrometer und auch den Vorschub eine Drehmaschine können Sie für diese Arbeit einspannen. Ob sich mehr Aufwand lohnt, bleibt in Anbetracht der beschränkten Genauigkeit des Instruments allerdings fraglich. Für grössere Genauigkeit sollten Sie eher die Messlatte - also die Sehne - verlängern.

Zeichnung und Fotos zum Ausdrucken (Format A4, 77kB)