• View
• Edit
• History
• Print

Weichenrechner

Viele Gartenbahner bauen ihre Weichen mit Augenmass und Handgewicht, 'from scratch', wie es in Übersee heisst: aus dem Handgelenk. Entsprechend können Sie viele Rezepte finden und ebenso viele hervorragende Weichen sehen. Ich habe meine erste Weiche auch so gebaut und dabei viel gelernt. Aber dann wollte ich es genauer wissen und habe die Weichengeometrie erkundet. So sind diese Seiten enstanden. Für die praktische Seite gehen Sie dann zur Seite Trassenbau?.

Weichengeometrie

• Bei Eisenbahnweichen besteht zwischen dem Kurvenradius des abzweigenden Geleises und der Spurweite ein fester Zusammenhang.
• Aus diesen beiden Grössen lässt sich der Ablenkwinkel, also der Winkel des Herzstücks berechnen.
• Im englischen Sprachraum wird statt des Ablenkwinkels die Weichennummer gebraucht, sie ist der Cotangens des Ablenkwinkels.

Diese Seiten beschäftigen sich mit diesen Zusammenhängen. Wenn Ihr Trigonometrie-Unterricht wie bei mir weit zurückliegt, finden Sie hier Hilfe: Wikipedia: sehr ausführliche und auch verständliche Seite

Berechnen des Ablenkwinkels aus Ablenkradius und Spurweite

Die Abbildung veranschaulicht die Geometrie einer (Rechts-)Weiche: Die geradeaus führenden Schienen sind Tangenten an die Kreise der abzweigenden Schienen. Wo die Tangenten den Kreis berühren (Punkte A und A'), sind die Zungenspitzen, wo die äussere abzweigende Schiene die geradeaus laufende kreuzt (Punkt B), liegt die Spitze des Herzstücks. Zusammen mit dem Zentrum des Kreises spannen diese Punkte das rote Dreieck auf, das beim Punkt A einen rechten Winkel hat.

ACHTUNG: Es spielt für diese Betrachtungen keine Rolle, ob das abzweigende Geleise nach dem Herzstück in die Tangente am Punkt B übergeht (also geradeaus weiterführt) oder weiter dem Kreis folgt!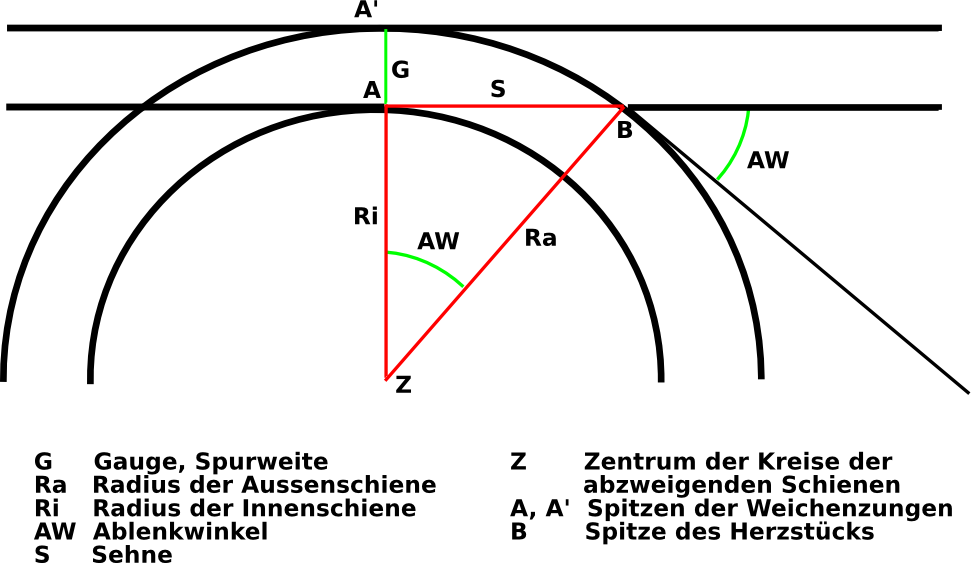

Nach Pythagoras ist der Abstand zwischen den Zungenspitzen und der Spitze des Herzstücks

   S = √ Ra² - Ri² (Sehne)

Der Cotangens des Ablenkwinkels ist dann

   cot(AW) = Ri / S 

Dieser Wert entspricht der im anglelsächsischen Raum beliebten Weichennummer N.

Und der Ablenkwinkel ergibt sich zu

   AWrad = arccot (cot(AW))  im Bogenmass Radians

beziehungsweise zu

   AWgrad = AWrad * 180 / π  in Graden

Berechnen der Weichennummer = Cotangens des Ablenkwinkels an einer vorhandenen Weiche

Die nebenstehende Zeichnung stellt ein WeichenHerzstück dar, die roten Geraden sind Hilfslinien. Die Gerade B-b ist die Winkelhalbierende des Ablenkwinkels AW, die Gerade a-c steht senkrecht auf dieser. Der Cotangens dieses Winkels, also die Weichennummer ergibt sich dann zu:

    B-b / 2 * a-b    mit grosser Genauigkeit oder

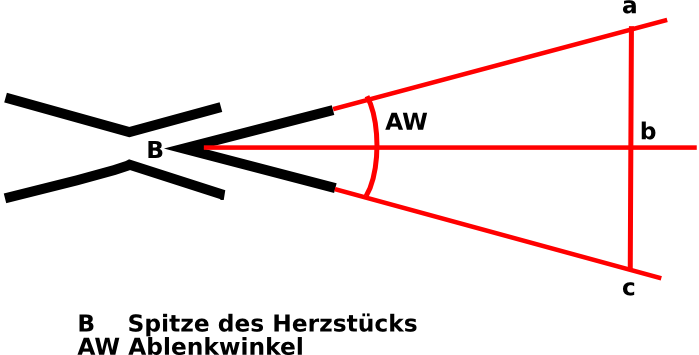    B-c / a-b        als Näherung für kleine Winkel AW

Weitere Näherungsformeln

Beim Stöbern nach Hinweisen bin ich noch auf folgende Formeln gestossen, die den Zusammenhang zwischen Weichennummer, Spurweite und Ablenkradius betreffen. Sie sind allerdings nur für Überschlagsrechnungen geeignet, ich gebe sie Ihnen zu treuen Handen:

Weichennummer errechnet aus Abzweigradius R und Spurweite G

    N = √ R / 2 * G      R und G in Millimetern

Oder aufgelöst nach R:

    R = 2 * G * N * N          R und G in Millimetern

Zusammenfassung und Bemerkungen

• Die Weichennummer und der Ablenkwinkel stehen in einem festen Zusammenhang unabhängig von der Spurweite: Die Nummer ist der Cotangens des Ablenkwinkels
• Bei gegebener Weichennummer ergibt eine grosse Spurweite einen grossen Radius und umgekehrt
• Bei Gartenbahnen werden wenn möglich keine kleineren Ablenkwinkel als N = 4 entsprechend 14° verwendet, Feldbahnen verwenden Ablenkwinkel bis N = 2.5 entsprechend 20°

Interessante Weichenseiten

• Gleisbau-Welt
  Alles über den Gleisbau beim Vorbild
• IPRR: verschiedene Weichenrechner
  Seite der Island Pond Railroad (7¼" oder 7½") mit vielen Tips zum Bau und Betrieb einer Gartenbahn, Bau- und Erfahrungsberichte, Weichenrechner für verschiedene Weichenformen, mit Berechnung der Schwellen. Sehr informativ, aber leider in Englisch und in Zoll...
• Military Railways
  Handbuch aus dem Jahre 1917 mit detaillierten Angaben zu allen Bereichen des Eisenbahnbaus und -Betriebs, über 500 Seiten als PDF zum Herunterladen
• Georg Schreyers Large Scale Trains Page
  Georg Schreyer ist ein Spur 0 und 1-Bahner.
• Fast Tracks
  Aussergewöhnlicher Geleisebau in den Spuren H0 bis Z, also nichts für Gartenbahner. Unter dem Link finden Sie jede Menge von Zeichnungen von Weichen zum Herunterladen und Ausdrucken. Die Weichen sind #4 oder schlanker, für Feldbahner nur ausnahmsweise geeignet.
• The On-Line Magazine of Rideable Model Railroading
  Switch Building at Maricopa Live Steamers: Bill Lowe's ausführlicher und bebilderter WeichenbauKurs. Die Seite enthält weitere Artikel aus dem Magazin.
• WEBB, Dave: Building Points for the "Boulder Creek Tramway"
  Weichenbau in 7¼" - die Boulder Creek ist den australischen Werkbahnen auf zwei Fuss Spurweite nachempfunden (Massstab 1:3), sehr ausführliche Darstellung, viele Bilder, empfehlenswert!
• ERTELD, Rudolf: Weichenbau Spur 7
  Weichen aus Schienenprofil, Zungen aus Flacheisen, Herstück geschweisst, für Feld-/Waldbahnen, GARTENBAHNEN 2/2004
• WIEGAND, Wolfgang: Weichenbau in Spurweite 184mm
  Weichen aus Schienenprofil, Zungen aus Schienenprofil, Herzstück Laserschnitt, anspruchsvolle Herstellung, GARTENBAHNEN 3/2002